When the purpose of a study is to evaluate the performance of a group of stimuli (concepts, products, or services) and each of the stimuli are rated by respondents, at the time of analysis, we should question the level of performance
of these items or trials.
Indeed, since these stimuli are most often assessed sequentially, part of these performances could be explained by the way these items and trials were assessed.
In particular, the position of these items or trials in the sequence may introduce 2 types of bias, namely:
✓ Order effect : Effect related to the number of times an item was assessed at each rank.
✓ Carryover effect : Effect related to the number of times an item has been tested after another (rank 1 carryover). The carry-over effect exists from level 1 (item immediately following another), to rank n (item following another, after having assessed n-1 other items before).
In order to control these biases, the field of experimental design allows to control these effects.
Let's conduct a concept test with 5 new offers evaluated by a panel of 100 respondents. The graph below summarizes the means of the concepts by evaluation rank as well as the standard deviations.
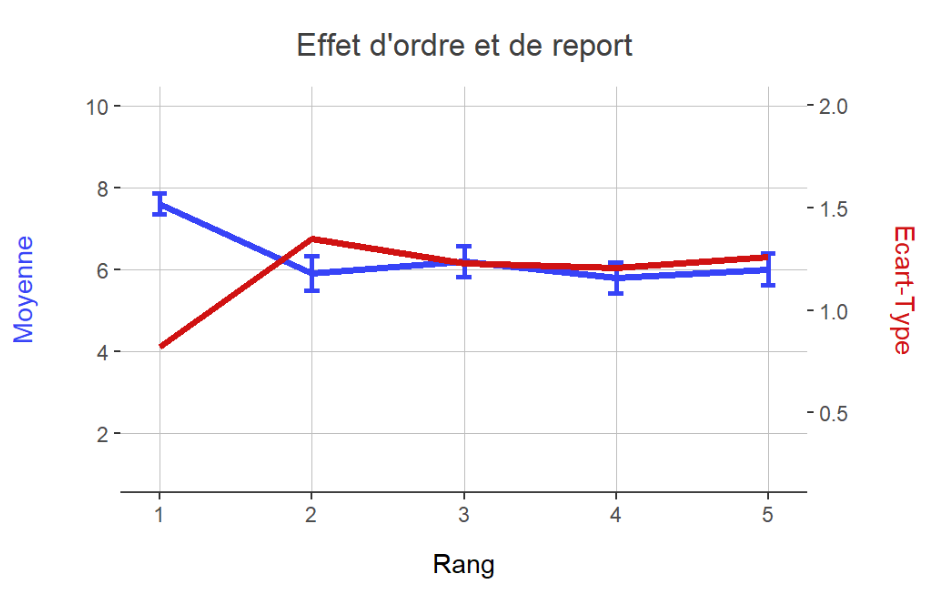
This graph shows that, on average, the score of the concepts at rank 1 is significantly different from the averages of the same concepts evaluated on the other ranks. Faced with this type of problem, 2 strategies are available:
✓ Pure monadic :
Respondents will rate only one concept. A part of the sample surveyed evaluates one and only one concept. This requires increasing the sample size by creating a sub-sample for each concept. It will also be necessary to match these sub-samples on structural variables such as socio-demographic variables in order not to bias the analysis with structural problems of the sample.
✓ Monadic sequential :
All respondents in the sample rate all concepts. During the analysis, you can decide to keep only the scores of the concepts evaluated from rank 2 to 5, or consider that on average all the concepts have undergone the same evaluation bias at rank 1, and therefore that on average the concepts are comparable between them.
Experimental designs
The main interest of using experimental designs during a survey is to control the biases related to :
✓ order effects
✓ carryover effects
within a specific sample, or even within several subsets of the sample studied.
This study protocol is to be used when the same individual is subjected to several stimuli in a sequential manner. The stimuli can be concepts, products, services, therapeutic treatments, etc.
The stimulus presentation plan is drawn up before the survey phase. This plan should be integrated into the questionnaire programming if it is computerized.
Prior to data collection, taking the time to build a balanced design globally and/or by sub-target is fundamental. This approach guarantees study results that are not biased by order and/or carryover effects.
What tools are available to build a successful presentation plan?
✓ Rotation :
Items are always assessed in the same order, but the 1st item is always different. This method does not control for carryover effects.
✓ Pure randomisation :
This is the simplest but least reliable method. Perfect balance can never be guaranteed, unless the sample size is increased considerably, especially if sub-samples are to be compared.
✓ Complete Block Designs (CBD) :
All respondents rate all products. The design is orthogonal across the entire sample and stimuli. The total number of stimuli to be tested can be tiring for respondents and reduces the quality of the data collected.
✓ Incomplete Balance Designs (IBD) :
Each respondent evaluates a subset of the stimuli studied. In the overall sample, each stimulus as well as pairs of stimuli are evaluated the same number of times.
Complete Block Designs (CBD)
✓ Latin Squares :
All the S stimuli are evaluated by the respondents. Each stimulus is evaluated the same number of times at each rank, and thus at the global level of the sequence. The number of respondents R is a multiple of the number of stimuli. This type of design does not control for carryover effects.
✓ Williams Latin Squares :
These plans allow, with a limited number of sequences, to control the order effects, and then the first-order carryover effects of the set of stimuli. The construction of these designs is simple. For an even number S of stimuli, we need R = S respondents to balance the plan. For an odd number S of stimuli, one needs R = 2 * S respondents to balance the plan.
✓ MOLS Designs :
Mutually Orthogonal Latin Squares control for the order effect, and carryover effects of all stimuli in all positions in the sequence. These designs are balanced over a larger number of respondents than Williams Latin Squares.
Incomplete Balance Designs (IBD)
✓ Incomplete Balance Designs (IBD) :
To construct a Balanced Incomplete Block design, we use all combinations of N stimuli among S stimuli to be distributed among R respondents.
| N = 3 | Stimuli (S) | |||
| Respondant (R) | A | B | C | D |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
IBD designs allow the evaluation of a large number of stimuli, controlling for respondent fatigue.
The IBD design should be coupled with a Williams Latin square or Latin square to control order and carryover effects. The main limitation of IBD is that there is not always a balanced design for all configurations (R, N, S).
✓ Incomplete Balance Designs (IBD) from MOLS designs :
From a MOLS design, we can select a subset of columns from the base design and we will obtain an incomplete block design balanced on order and carryover effects of order 1.
✓ Optimal Designs :
Since complete balanced designs do not exist for all combinations of (R, N, S), we can construct (R, N, S) designs by accepting to degrade some statistical parameters. These designs are constructed by successive permutations of stimuli taken 2 by 2, seeking to optimize the criteria of optimality measured by the analysis of the variance of the effects of the stimuli.
The optimal criteria are numerous. Let’s just mention the 2 usual criteria :
⚬ D-optimal, optimization of the X'X-1 trace
⚬ A-optimal, optimization of the determinant of X'X...
You have a design of experiments project and need help, contact us.