La corrélation est un indicateur statistique largement répandu en analyse de données, en particulier dans les études marketing type enquête de satisfaction, que l'étude soit baromètrique ou non, ou bien encore en innovation produit ou service. De par la simplicité de sa mise en oeuvre, c'est bien souvent le 1er outil statistique utilisé.
Nous nous proposons dans cet article de discuter et préciser l'usage de la corrélation dans l'univers des études. Nous proposerons des alternatives plus adaptées en fonction du niveau stratégique de l'étude.
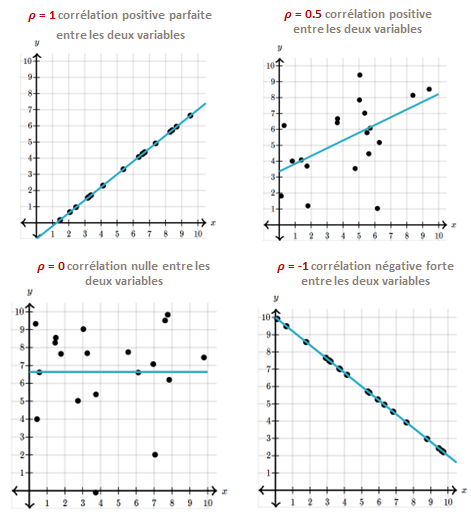
La corrélation, au sens de Spearman, est un outil statistique qui mesure la relation existante entre 2 variables.
✓ Une corrélation positive signifie que 2 variables varient simultanément dans le même sens.
✓ Une corrélation négative signifie que 2 variables varient simultanément dans le sens opposé.
✓ Une corrélation nulle signifie que 2 variables sont indépendantes l'une de l'autre.
La corrélation est un indicateur statistique couramment utilisé en marketing pour apprécier l'importance, l'impact, d'une variable sur une autre. En ce sens, l'utilisation de la corrélation permet de contourner les biais cognitifs inhérents à la nature humaine lorsque nous posons la question directement aux répondants dans un contexte d'étude. En s'abstenant de poser une question d'importance déclarée directement aux répondants, nous pouvons tout de même, de façon dérivée, calculer cette importance entre deux variables via le calcul de la corrélation.
Ne pas poser les questions directement aux répondants, permet d'optimiser la taille du questionnaire dans un contexte d'enquête.
La corrélation peut être utilisée pour :
✓ Identifier la force de la relation d'une variable sur une autre,
✓ Hiérarchiser les variables, par leur niveau de corrélation sur une variable cible, les unes par rapport aux autres,
✓ Editer une matrice importance / satisfaction,
✓ Choisir les variables à inclure dans un modèle de prédiction,
✓ ...
L'usage de la corrélation a toutefois ses limites. En particulier, la corrélation :
✗ Ne signifie pas causalité,
✗ Peut être influencée par des données exogènes,
✗ Ne tient pas compte des interactions entre variables.
De plus, dans le cadre d’une étude de type barométrique, l’utilisation de la corrélation en phase d’analyse, peut se révéler contre productive.
Imaginons que lors d’une première analyse, la corrélation a permis d’identifier les leviers de la satisfaction. Votre client met en place un plan d’actions pour travailler les leviers en question.
Une seconde enquête permet de mettre en évidence une amélioration significative de la performance de ces leviers. Ce faisant, et de façon tout à fait mécanique, la variance de ces leviers diminue. La corrélation de ces leviers à la satisfaction diminue donc également pour tendre vers une relative indépendance des variables.
Le client conclue alors que d’autres leviers sont à travailler en priorité dans un nouveau plan d’actions, et met de côté les leviers initiaux de la satisfaction.
Ici réside l’erreur d’interprétation.
Il existe d’autres indicateurs statistiques ou outils permettant de valoriser au mieux les données collectées et éviter les pièges de l’usage de la corrélation. Nous vous présentons ici 3 alternatives, de la plus simple à la plus complexe, de la moins chère à la plus chère mais avec une très forte valeur ajoutée :
✓ Les corrélations partielles :
Mesure la relation entre deux variables tout en contrôlant l'influence des autres variables incluses dans l'analyse = tient compte des interactions entre variables. Cet indicateur permet une compréhension plus nuancée de la relation entre deux variables.
Toutefois cet outil ne permet pas d'identifier les causalités, leur sens, et est très dépendant des variables incluses dans l'analyse, c'est à dire potentiellement influencée par des données exogènes.
✓ Les équations en modèle structurel :
Outil statistique utilisé pour représenter et analyser les relations causales entre les variables. Les équations en modèle structurel utilisent une combinaison d'analyse factorielle et de régression multiple pour déterminer et estimer les relations entre les variables.
Les équations en modèle structurel ne représentent pas toujours fidèlement les relations complexes entre les variables et peuvent être sensibles aux données manquantes ou aux spécifications incorrectes du modèle définies par l'analyste.
✓ Les réseaux Bayesien :
Cet outil permet de représenter et analyser les relations causales entre les variables injectées dans l'analyse. Cet outil utilise une approche probabiliste et l'inférence bayésienne pour représenter et mettre en évidence les relations existant entre les variables analysées.
Les réseaux Bayesien peuvent :
✔ Représenter des relations complexes entre variables,
✔ Gérer les données manquantes et les relations incertaines,
✔ Etre mis à jour à mesure que de nouvelles données sont disponibles.
Les réseaux Bayesien ont toutefois quelques inconvénients :
✗ La mise en œuvre peut être gourmande en temps de calculs,
✗ Son utilisation peut nécessiter des connaissances spécialisées pour préciser la structure et les probabilités du réseau.
✗ Et par conséquent, des coûts de mise en œuvre plus élevés.
Nous avons pu aborder dans cet atricle, de façon succinte, la notion de corrélation et ses éventuelles limites, comme dans le cas des études barométriques. Nous avons proposé 3 outils pour contourner les limites de la corrélation.
Au-delà des alternatives vues précédement, il existe entre le très simple, et le plus compliqué avec les réseaux Bayesien, des outils très abordables, tels que l'effets des attributs, l'analyse de leviers comparés, la matrice de Llosa dans le cas d'une étude de satisfaction ... et encore bien d'autres outils pour identifier les variables qu'il convient de travailler dans vos plans d'actions.
Vous avez besoin d'accompagnement pour trouver dans vos données les leviers d'amélioration de vos indicateurs de performance, contactez nous.