Lorsque l'objectif d'une étude est d'évaluer les performances d'un groupe de stimuli (concepts, produits ou services) et que chacun des stimuli sont évalués par des répondants, au moment de l'analyse, on doit se questionner...
quant au niveau de la performance de ces items ou essais.
En effet, ces stimuli étant évalués le plus souvent de façon séquentielle, une partie de ces performances pourrait être expliquée par la façon dont ces items et essais ont été évalués.
En particulier, la position de ces items ou essais dans la séquence peut introduire 2 types de biais, à savoir :
✓ Effet d'ordre : Effet lié au nombre de fois où un item a été évalué à chaque rang.
✓ Effet de report : Effet lié au nombre de fois où un item a été testé après un autre (report d'ordre 1). L'effet de report existe du niveau 1 (item suivant immédiatement un autre), au rang n (item suivant un autre, après avoir évalué n-1 autres items auparavant).
Afin de contrôler ces biais, le champ des plans de présentations (expérimental design) permet de maitriser ces effets.
Consédirons un test de concept avec 5 nouvelles offres évaluées par un panel de 100 répondants. Le graphique ci-dessous synthétise les moyennes des concepts par rang d'évaluation ainsi que les écart-types.
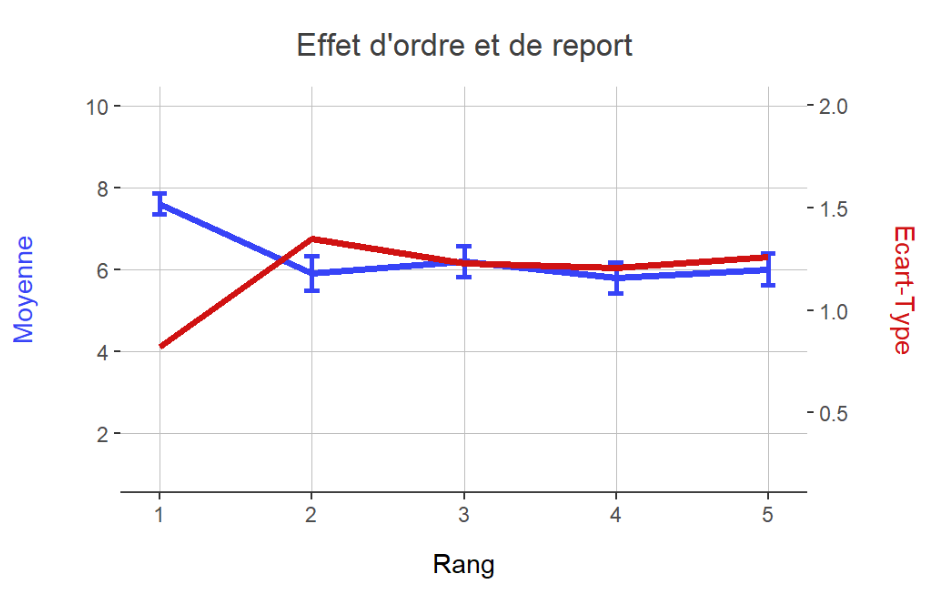
Ce graphique nous apprend qu'en moyenne la note des concepts au rang 1 est significativement différente des moyennes des mêmes concepts évalués sur les autres rangs. Face à ce type de problème, 2 stratégies sont possibles :
✓ Monadique pure :
Les répondants évaluent un seul concept. Une partie de l'échantillon interrogé évalue un seul et unique concept. Cela nécessite donc d'augmenter la taille d'échantillon interrogé en créant un sous-échantillon par concept. Il conviendra également d'apparier ces sous-échantillons sur des variables de structure telles que les variables socio-démographiques pour ne pas biaiser l'analyse avec des problèmes structurels de l'échantillon.
✓ Monadique séquentiel :
Tous les répondants de l'échantillon évaluent tous les concepts. A l'analyse, vous pouvez décider de ne conserver que les scores des concepts évalués du rang 2 à 5, ou bien considérer qu'en moyenne tous les concepts ont subi le même biais d'évaluation au rang 1, et donc qu'en moyenne les concepts sont comparables entre eux.
Plans de présentation
L’intérêt principal d’utiliser des plans de présentation lors d’une enquête est de maitriser les biais liés aux :
✓ Effets d'ordres
✓ Effets de reports
au sein d’un échantillon spécifique, voire au sein de plusieurs sous-ensembles de l’échantillon étudié.
Ce protocole d’étude est à utiliser lorsqu’on soumet à un même individu plusieurs stimuli de façon séquentielle. Les stimuli peuvent être des concepts, des produits, des offres de services, des traitements thérapeutiques, etc.
Le plan de présentation des stimuli est construit en amont de la phase d’enquête. Ce plan est à intégrer lors de la programmation du questionnaire si celui-ci est informatisé.
En amont de la récolte des données, prendre le temps de construire un plan équilibré au global et / ou par sous-cible est fondamental. Cette approche garantit des résultats d’études non biaisés par des effets de présentation.
Quels sont les outils disponibles pour construire un plan de présentation performant ?
✓ Rotation :
Les items sont évalués toujours dans le même ordre, mais le 1er item est toujours différent. Cette méthode ne permet pas de contrôler les effets de report.
✓ Aléatoire pure (Randomisation) :
C'est la méthode la plus simple mais la moins fiable. On ne peut jamais garantir l'équilibre parfait, sauf à considérablement augmenter la taille d'échantillon interrogé, en particulier si l'on doit comparer des sous-échantillons.
✓ Blocs Complets :
Tous les répondants évaluent tous les produits. Le plan est orthogonal au travers de l'ensemble de l'échantillon et des stimuli. Le nombre total de stimuli à tester peut être lassant pour les répondants et diminue la qualité des données ainsi collectées.
✓ Blocs Incomplets Équilibrés (BIE) :
Chaque répondant évalue un sous-ensemble des stimuli étudiés. Au global de l'échantillon, chaque stimuli ainsi que les paires de stimuli sont évalués le même nombre de fois.
Blocs Complets
✓ Les Carrés Latins :
L'ensemble des S stimuli sont évalués par les répondants. Chaque stimuli est évalué le même nombre de fois à chaque rang, et donc au global de la séquence. Le nombre de répondants R est un multiple du nombre de stimuli. Ce type de plan ne contrôle pas les effets de report.
✓ Les Carrés Latins de Williams :
Ces plans permettent avec un nombre restreint de séquences de contrôler les effets d'ordre, puis les effets de report d'ordre 1 de l'ensemble des stimuli. La construction de ces plans est simple. Pour un nombre S pair de stimuli, il faut R = S répondants pour équilibrer le plan. Pour un nombre S impair de stimuli, il faut R = 2 * S répondants pour équilibrer le plan.
✓ Les plans de MOLS :
Les Carrés Latins Mutuellement Orthogonaux contrôlent l'effet d'ordre, et les effets de report de tous les stimuli dans toutes les positions de la séquence. Ces plans sont équilibrés sur un plus grand nombre de répondants que les carrés latins de Williams.
Blocs Incomplets Équilibrés
✓ Blocs Incomplets Equilibrés (BIE) :
Pour construire un plan en Bloc Incomplet Équilibré, on utilise toutes les combinaisons de N stimuli parmi S stimuli à distribuer parmi R répondants.
| N = 3 | Stimuli (S) | |||
| Répondant (R) | A | B | C | D |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
Les plans de type BIE permettent d’évaluer un grand nombre de stimuli, en contrôlant la lassitude des répondants.
Il convient de coupler le plan en BIE avec un carré latin ou carré latin de Williams pour contrôler les effets d’ordre et de report. La limite principale des BIE est qu’il n’existe pas toujours de plan équilibré pour toutes les configurations (R, N, S).
✓ Blocs Incomplets Equilibrés (BIE) à partir de plans de MOLS :
A partir d’un plan de MOLS, nous pouvons sélectionner un sous-ensemble de colonnes du plan de base et nous obtiendrons ainsi un plan en bloc incomplet équilibré sur les effets d’ordre et de report d’ordre 1.
✓ Plans Optimaux :
Les plans complets équilibrés n’existant pas pour toutes les combinaisons de (R, N, S), nous pouvons construire des plans (R, N, S) en acceptant de dégrader certains paramètres statistiques. Ces plans sont construits par des permutations successives de stimuli pris 2 à 2 en cherchant à optimiser des critères d’optimalités mesurés par l’analyse de la variance des effets des stimuli.
Les critères optimaux sont nombreux. Citons juste les 2 critères usuels suivants :
⚬ D-optimal, optimisation de la trace de X'X-1
⚬ A-optimal, optimisation du déterminant de X'X...
Vous avez un projet de plan d'expériences et besoin d'aide, contactez nous.